Enregistrement, avec l'ordinateur, des oscillations de relaxation
d'un vase de Tantale
Denis Gauthier
Lycée Bernard Palissy
164 Boulevard de la Liberté, 47000 Agen
Cet enregistrement nécessite la réalisation d'une tension proportionnelle à la hauteur de liquide dans le vase.
J'avais déjà obtenu cette tension en utilisant le rhéostat d'une jauge à essence de voiture que l'on place dans le vase et dont le flotteur fait varier la résistance avec le niveau de l'eau (actes des 7èmes journées Informatique et pédagogie des Sciences Physiques de Bordeaux, février 1996). Mais la grandeur de cette jauge obligeait à utiliser un récipient et un siphon de grande taille ce qui donnait, à l'amorçage et au désamorçage, un régime transitoire un peu long perturbant les courbes.
On peut aussi créer cette tension en utilisant une solution diluée de sulfate de cuivre et en transformant le vase en cuve rhéographique d'écartement variable, avec un plaque de cuivre placée au fond et l'autre, sous un bouchon, suivant le niveau du liquide (Eric Castet, BUP n° 792, mars 1997).
La sortie récente d'un capteur de pression différentielle ± 20 mBar CD2000PaD1 (Langage et Informatique, 8 avenue Edouard Serres, BP 11 31771 Colomiers Cedex) rend la réalisation de cette tension très simple et très fiable. Ce capteur donne une tension (V) de même valeur numérique que la différence de pression (mBar) entre le fond du vase et la pression atmosphérique : on a donc u(V) numériquement égale à z(cm).
1- Dispositif :
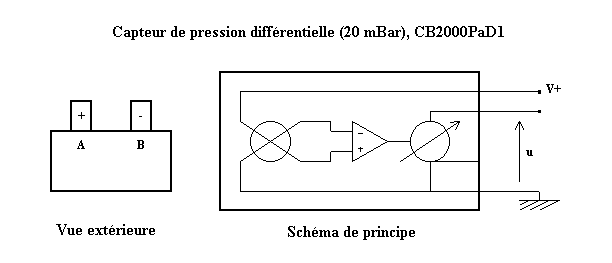
1-1 Le capteur :
Il se présente sous la forme d'un boitier parallélépipédique de petites dimensions (L = 6 cm ; l = 3 cm ; h = 1,8 cm) surmonté de deux petits cylindres (f = 4,8 mm) sur lesquels on adapte des tuyaux souples pour recevoir les pressions entre lesquelles on mesure la différence : port A (+) relié au point de pression la plus forte et port (B) relié au point de pression la plus basse.
Ce capteur est formé d'un pont piézorésistif implanté sur un substrat de silicium, déséquilibré par l'existence d'une différence de pression entre A et B, et d'un dispositif de traitement donnant décalage et amplification. Il est relié par un prise DB 9 (ou minidin) à la carte du convertisseur analogique-numérique dont il utilise la tension 5 V comme alimentation V+ et à laquelle il donne la tension u.

Figure 1
1-2 Le montage avec le vase :
Le vase de Tantale est réalisé avec une cuve en verre cylindrique de la collection d'hydrostatique (diamètre intérieur, D = 13,5 cm ; hauteur 21,5 cm) munie d'une ouverture vers le bas à laquelle on adapte un tube en U recoudé (diamètre intérieur, d = 1,2 cm ; h0 = 11 cm). On alimente le vase par un robinet de la distribution urbaine équipé d'un tuyau caoutchouc pour éviter le clapot. Le port A (+) est mis à la pression du fond du vase par un tuyau souple et une pipette de verre fixée au vase ; le port B (-) est à la pression atmosphérique.
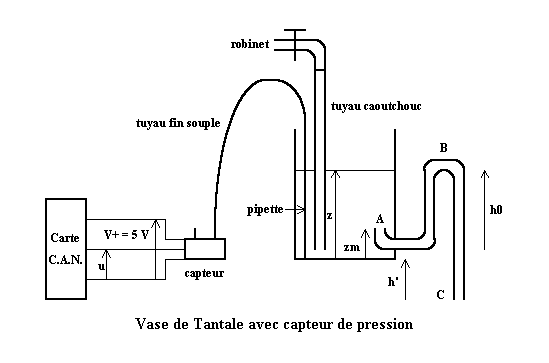
Figure 2
Le débit D0 du robinet est réglé assez faible pour permettre la vidange et un bon désamorçage du siphon. Le deuxième coudage, côté A, est difficile à réaliser ; il n'est pas indispensable mais il permet un désamorçage du siphon plus net.
2- Enregistrement avec SYNCHRONIE :
2-1 De la courbe des oscillations, z(t) et de la vitesse vz = dz/dt :
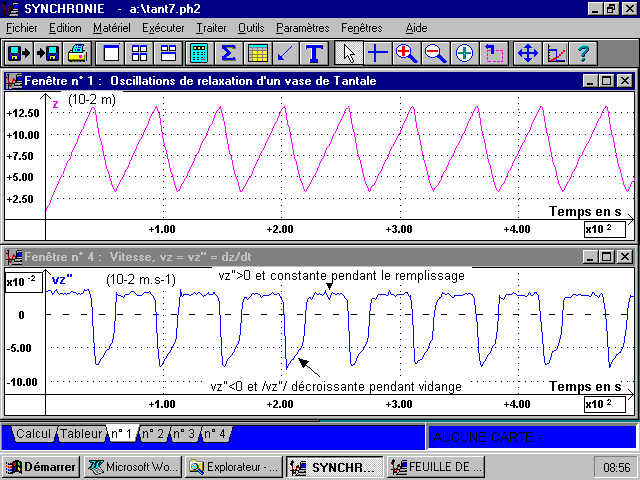
Figure 3
2-2 De la trajectoire de phase vz(z) :
2-2-1 Courbe :
Voir figure 4. Cette figure contient une modélisation de la vitesse, vz = vz2, au cours de la vidange, traitée au paragraphe suivant.
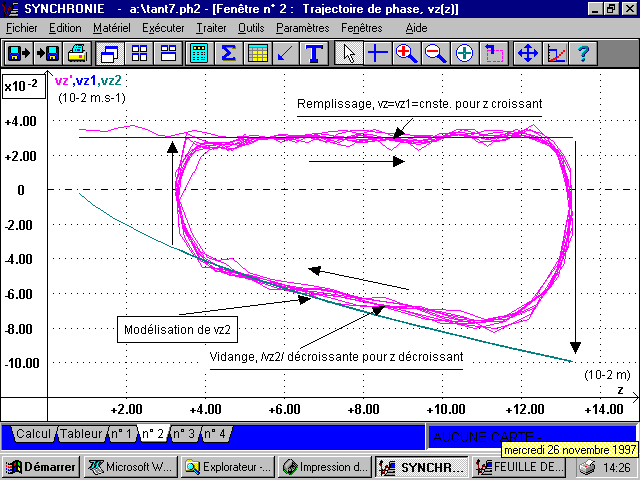
Figure 4
3- Modélisation de vz au cours de la vidange :
3-1 Equation différentielle et expression de vz au cours des deux phases :
Cette équation est donnée, pour chaque phase, par la conservation, entre t et t + dt, du volume de liquide d'une partie élémentaire du vase (section S et épaisseur dz) ; on en tire, chaque fois, l'expression de vz = dz/dt. On appelle D0, le débit constant du robinet et vC la vitesse d'écoulement du liquide à la sortie C du siphon.
* Remplissage :
D0.dt = S.dz et vz1 = dz/dt = D0/S (1)
* Vidange :
S.dz = D0.dt - s.vC.dt et vz2 = dz/dt = D0/S - (s/S).vC = vz1 - (s/S).vC (2)
Dans ce dispositif on a, S >> s, et on peut assimiler le régime permanent au régime permanent d'un fluide parfait. L'application du théorême de Bernoulli permet d'exprimer vC par la relation, ![]() .
.
3-2 Conséquences :
* Remplissage :
vz1= D0/S = constante > 0
C'est bien ce que l'on constate sur les courbes vz(t) de la figure 3 et vz(z) de la figure 4, pour les phases de remplissage. Le bruit des paliers de la courbe vz(t) est du à la dérivation de la suite discrète des valeurs de z qui accentue les petites imperfections de z ; il est atténué en utilisant le paramètre MOYENNE de la rubrique ACQUISITION (pour chaque mesure demandée, le logiciel prend pour valeur la moyenne de n acquisitions successives, ici 8) et en effectuant ensuite un lissage de la courbe.
On relève, vz1 =3,0 x 10-2 cm.s-1 = 3,0 x 10-4 m.s-1 et on en peut en tirer le débit du robinet :
D0 = vz1.S = vz1. p D2/4 = 0,0003 x p x (0,123)2/4 =3,6 x 10-6 m3.s-1 = 3,6 mL.s-1
* Vidange :
vz2 = vz1 - (s/S)![]() = vz1 - (d/D)2.
= vz1 - (d/D)2.![]() < 0
< 0
Dans cette phase, la hauteur d'eau z dans le vase diminue ; vC décroit et, avec, la valeur absolue de vz2
Ici aussi, c'est bien ce que l'on observe sur les courbes vz(t) de la figure 3 et vz(z) de la figure 4, pour les phases de vidange.
Remarque :
On pourrait avoir vC et par suite vz2 pratiquement constante en utilisant un dispositif dans lequel h' serait grand devant zmaximal.
3-3 Modélisation de vz2 :
3-3-1 Courbe vz2(z) :
Avec les paramètres du dispositif utilisé et en prenant la valeur expérimentale de vz1 = 0,03 cm.s-1, on peut exprimer vz2 par la relation : vz2 (cm.s-1) = 0,03 - 0,008![]() .
.
La FEUILLE DE CALCUL permet de tracer la courbe vz2(z) en programmant :
vz2= 0.03 -0.008*SQRT(19.6(0.03+z))
La courbe obtenue est représentée dans la figure 4.
3-3-2 Rapprochement avec la courbe expérimentale :
Dans le domaine de z correspondant au régime permanent de la vidange [3,7 cm ; 11,4 cm], on note une bonne coïncidence entre vz2 modélisé et vz2 expérimental de la trajectoire de phase.
Cette coïncidence est meilleure quand z diminue ; on peut expliquer cela par un régime mieux établi et une vitesse d'écoulement moins grande entrainant moins de frottements.
3-3-3 Conclusion :
Ce rapprochement donne une vérification expérimentale satisfaisante des approximations faites conduisant à l'application du théorème de Bernoulli et de l'expression, ![]() .
.
Le groupe académique Sciences-Physiques et Informatique