Sur deux définitions de la sphère

, Culture - Jean Pierre Kahane, Professeur émérite à l'Université Paris Sud - Membre de l'Académie des Sciences n°14, mars 2001

« La sphère de centre A et de rayon r est l'ensemble des points de l'espace situés à la distance r du point A ». C'est essentiellement la définition d'Euclide, un modèle de définition mathématique impeccable.

« La sphère est la figure la plus parfaite et la plus semblable à elle-même ». C'est ainsi que Platon, bien avant Euclide, explique que le Créateur ait fait choix de la sphère pour construire l'Univers. Ce n'est pas une définition mathématique, et elle est étrange à première vue - des traducteurs se sont posé la question : est-ce que toute figure n'est pas rigoureusement semblable à elle-même ?

Pour commencer l'étude de la sphère dans un cours de géométrie, la première définition est évidemment préférable. Elle est d'ailleurs riche de possibilités qui débordent le cadre de la géométrie élémentaire. Cependant elle est très loin de l'expérience commune : aucune boule, aucun ballon ne laisse voir son centre. C'est une abstraction mathématique, simple et puissante, mais qui a dû mettre longtemps à émerger dans l'esprit des hommes. On peut apprendre rapidement une telle définition, mais il faut du temps et du travail pour la comprendre.

La définition de Platon, par contre, se présente comme un constat et constitue un programme. Elle dit l'apparence, figure parfaite, et la propriété fondamentale, l'invariance par le plus grand groupe possible. Elle s'intègre dans une vision cosmogonique où figurent aussi les polyèdres réguliers : le cube (la terre), le tétraèdre (le feu), l'octaèdre (l'air), l'icosaèdre (l'eau), et le dodécaèdre, qui ressemble aux ballons à douze pièces fabriqués par les artisans athéniens, et qui a pu servir au Créateur pour façonner la sphère (c'est d'ailleurs l'idée de base de l'architecte Fuller pour construire la sphère de l'exposition universelle de Montréal, à cela près qu'il complète les douze pièces par des hexagones ; d'où le nom de fullerènes donné par les chimistes aux molécules de carbone ayant cette configuration).

Pour une figure bornée de l'espace, le plus grand groupe possible est celui de toutes les rotations admettant un point fixe donné. Donc la propriété d'être « la plus semblable à elle-même » conduit bien à l'idée du centre et à la définition d'Euclide.

L'expression « la plus parfaite » admet plusieurs interprétations. L'une d'entre elles est que l'on peut reconstruire l'ensemble de la sphère dès que l'on en connaît un petit morceau. Une fourmi arpenteuse, capable de se promener sur une surface selon les géodésiques, et de mesurer les angles a , b , g  et la surface s d'un petit triangle, sait reconnaître qu'elle est sur une sphère et calculer son rayon. Elle n'a qu'à appliquer la formule d'Albert Girard : .

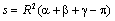Elle reconnaîtrait aussi bien si elle est sur une pseudosphère, dont la courbure est négative et constante, et que l'on représente souvent comme le demi-plan de Poincaré ; la formule est alors : .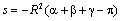

Et de façon générale, la fourmi arpenteuse a accès à la courbure de la surface sans sortir de la surface, comme nous avons accès à la courbure de l'univers sans sortir de l'univers. Girard, Lobatschevski, Poincaré, Einstein me paraissent ainsi, sans trop forcer le trait, dans l'héritage de Platon comme visionnaire des mathématiques. Platon, dont la philosophie peut être par ailleurs détestable, est un grand créateur de programmes. Euclide, comme plus tard Ptolémée, est un génial exécutant. Nous sommes les héritiers de l'un et de l'autre.