cine99

Utilisation d'un optocapteur pour l'étude cinétique de la réaction H₂O₂ + I^-,

Spectrophotomètre

Par Denis Gauthier, Lycée Bernard Palissy, 47000 Agen

1- Tracé des courbes cinétiques, en utilisant une photodiode et l'ordinateur :

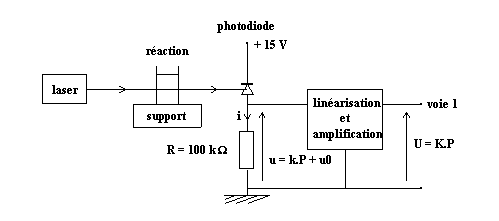
1-1 Dispositif :

La photodiode (BPW 34 B), polarisée en inverse, conduit un courant i qui, à température constante, est fonction affine croissante de la puissance lumineuse P (laser rouge de longueur d'onde, l = 670 nm) qu'elle reçoit ; i produit aux bornes de R une tension, u = R.i = k.P + u₀. Après traitement par un dispositif électronique de linéarisation et d'amplification, on obtient une tension U de quelques Volts, fonction linéaire de P, U = K.P, qui est envoyée en voie 1 d'un ordinateur muni d'une carte convertisseur analogique-numérique et du logiciel d'acquisition Synchronie. Voir détails techniques sur le BUP n° 784 de mai 1996 : montage pages 937 à 942 et réglages pages 922-923.

La réaction est réalisée dans les mêmes conditions que dans le TP, où son évolution est suivie par iodomètrie : 25 mL sol. H₂O₂ (4,0 x 10^-2 mol.L^-1) + 0,83 mL sol. H₂SO₄ (3,0 mol.L^-1) + 25 mL sol. KI (2,5 x 10^-1 mol.L^-1), mélangés dans une cuve à faces parallèles à t = 0 ; et l'acquisition de U(t) est ici aussi programmée sur une durée de 50 min = 3000 s.

1-2 Tracé des courbes n(I₂)(t) et n(H₂O₂)(t) à partir de U(t) :

1-2-1 Principe :

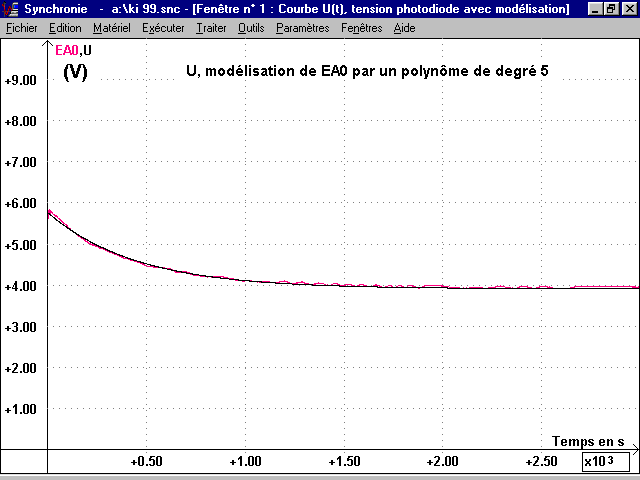
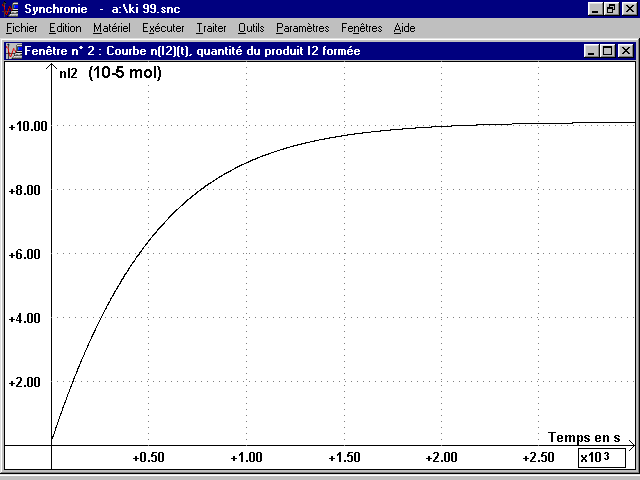
* La puissance lumineuse P, reçue par la photodiode, diminue à mesure que la réaction se déroule et que n(I₂) (espèce colorée) augmente : le milieu réactionnel devient plus sombre et plus absorbant pour la lumière. La courbe U(t) montre que U décroît suivant une allure exponentielle : il existe donc une relation entre U et n(I₂).

* Cette relation est trouvée expérimentalement de la façon suivante : pour un même date t, le tableau des mesures réalisées en TP donne la valeur de n(I₂) et la courbe U(t) (avec le pointeur du logiciel) donne la valeur de U (voir copie écran du tableur de Synchronie).

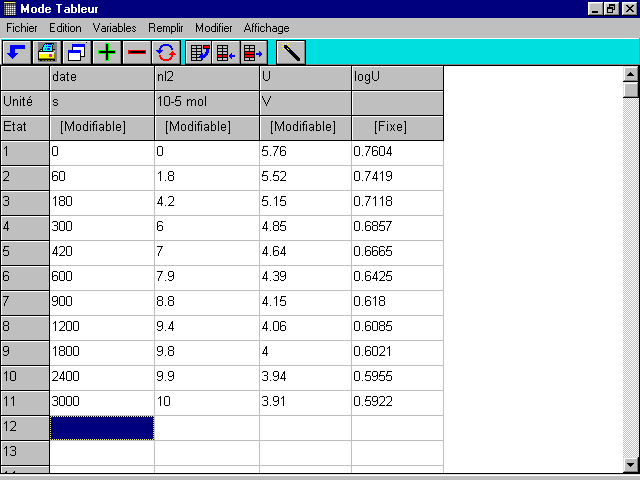
Ce tableau donne les valeurs correspondantes de n(I₂) et de U et permet de tracer une courbe, logU = f{n(I₂)} (voir page suivante).

Cette courbe peut-être modélisée par une fonction affine :

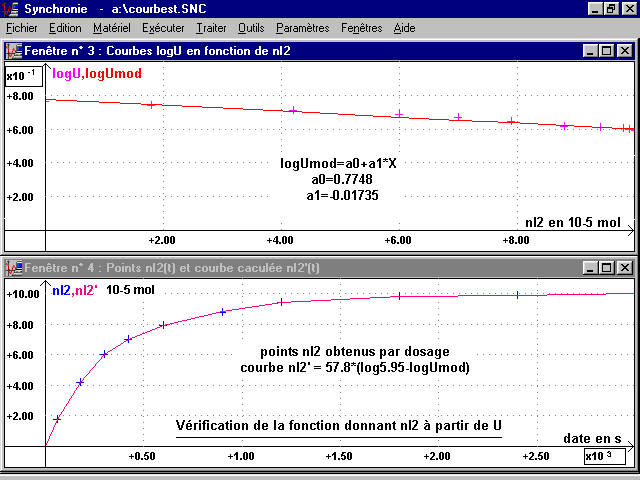
logU = a0₀ + a₁.nI2 = 0,7748 - 0,01735*nI2

avec a₀ = 0,7748 = logU pour nI2 = 0 (espèce colorée absente) = logU₀ et U₀ = 5,95 V

log U = log U₀ + a₁.nI₂ soit log (U/U₀) = a1.nI₂ et U/U₀ = 10^a1.nI2

d'où U = U₀ x 10^a1.nI2 = U₀x 10^{-a .nI2}

avec U tension pour une valeur de n(I₂) ¹ 0 (espèce colorée présente) et a = - a₁= 0,01735 = constante (pour une espèce chimique, une longueur d'onde et une longueur de trajet dans la cuve, données). Cette relation est une expression de la loi de Beer-Lambert.

Sous la forme, log (U / U₀) = - a .n(I₂), elle permet de calculer nI₂, connaissant U_{0 ,}U et a :

n(I₂) = - (1 / a ).log( U / U₀) = (1 / a ).log (U₀/U)

On peut donc, à partir de la courbe U(t), obtenir la courbe nI₂(t) que l'on peut rapprocher des points nI₂(t) du dosage (voir page suivante) ; puis la courbe n(H₂O₂)(t).

1-2-2 Courbes :

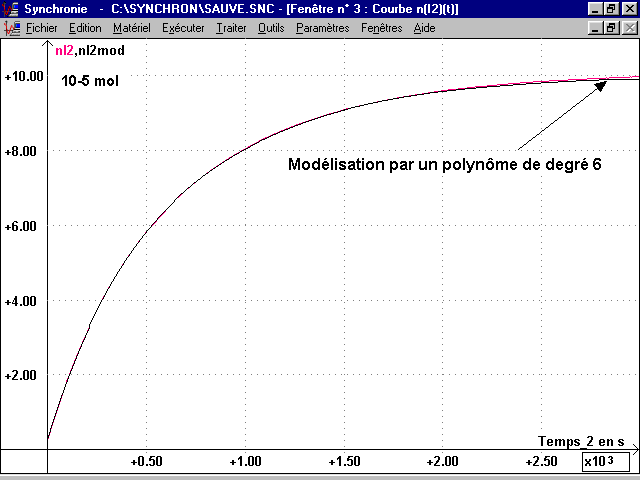
On utilise la courbe U(t) enregistrée et modélisée Umod(t) (fonction polynôme de degré 4 ou 5) pour obtenir un meilleur tracé des courbes cinétiques.

a) n(I2)(t) :

La modélisation de logU(nI₂) indique a = - a1 = 0,01735 et 1 / a = 57,8 (avec nI2 en 10^-5 mol) et U₀ = 5,95 V. On écrit dans la feuille de calcul du fichier de Synchronie où on a enregistré et modélisé U(t) :

nI2 = 57.8*log(5.95/Umod) {10^-5 mol}
Courbe représentée sur la page 4.

b) n(H₂O₂)(t) :

On tape dans la feuille de calcul :

nH2O2 = max(nI2) - nI2
Courbe représentée sur la page 4.

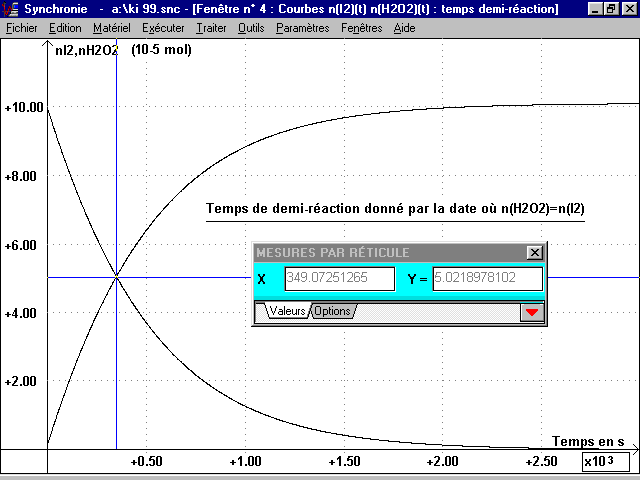
c) n(I₂)(t) et n(H₂O₂)(t) sur le même graphique :

L'intersection de ces deux courbes donne l'instant où la moitié du réactif limitant H₂O₂ a disparu et permet de connaître le temps de demi-réaction t _1/2 " 350 s (voir page 5).

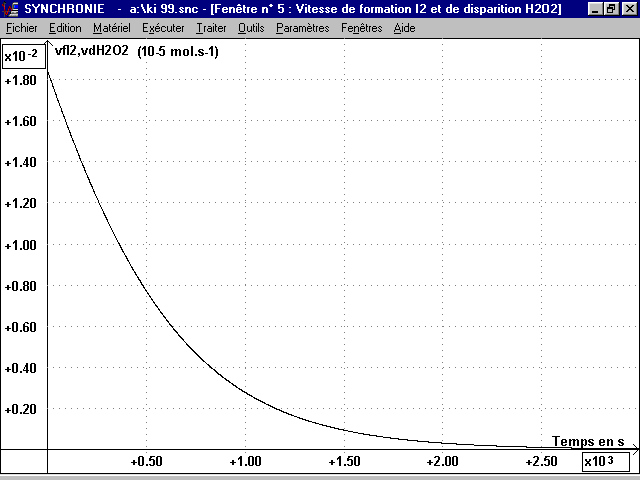
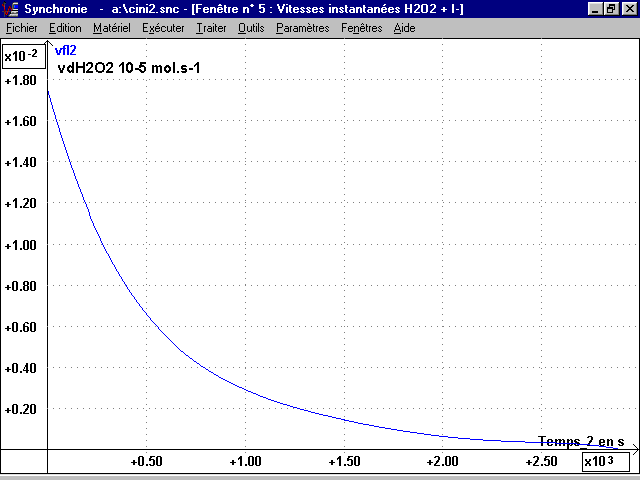
1-3 Tracé des courbes v_f (I₂)(t) et v_d(H₂O₂)(t) :

On écrit sur la feuille de calcul de Synchronie :

vfI2 = deriv(nI2,t) et vdH2O2 = -deriv(nH2O2,t)
Ces deux courbes identiques sont représentées par le même graphique page 6.

2- Spectrophotomètre :

2-1 Principe :

* Le spectrophotomètre utilise le même principe que le dispositif employé au § 1 : source de radiation monochromatique et capteur optoélectronique. On peut ici faire varier la longueur d'onde et un enregistrement préliminaire permet de choisir la valeur de l qui donne l'absorption maximale pour l'espèce colorée utilisée.

* Nous avons établi expérimentalement la loi de Beer-Lambert sous la forme U = U₀x 10^{-a n(I2}) avec U tension de sortie du montage amplificateur pour n(I₂) ¹ 0 (avec espèce colorée) et U₀tension pour n(I₂) = 0 (sans espèce colorée). Cette relation donne, en remplaçant n(I₂) par C(I₂).V = C.V:

U = U₀ x 10^{-a CV} = U₀ x 10^{-a 'C} avec a ' = a V

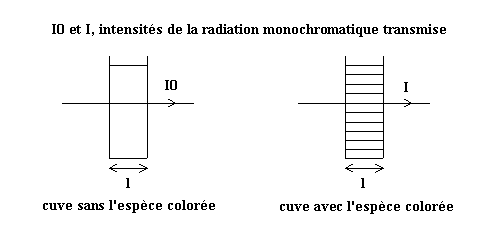
La tension, à la sortie du montage amplificateur qui accompagne le capteur optoélectronique, est proportionnelle à la puissance lumineuse reçue par le capteur, qui est elle même proportionnelle au carré de l'intensité lumineuse reçue I. La relation précédente donne, avec I₀ intensité transmise par la cuve en l'absence d'espèce colorée et I intensité transmise par la cuve avec l'espèce colorée à la concentration C :

U / U₀ = (I / I₀)² = 10^{-a '} et 2 log (I₀ / I) = a '.C

On appelle, par définition, absorbance A = log (I₀ / I) (nombre sans unité) et on en déduit :

A / C = a ' / 2 = constante

Pour une longueur d'onde l donnée, l'absorbance est donc proportionnelle à la concentration de l'espèce colorée ; le coefficient de proportionnalité dépend de l'espèce, de l et de la longueur l parcourue par la radiation dans la solution contenant cette espèce :

avec e l = contante pour une espèce colorée et un longueur d'onde données.

D'où la relation, valable pour des solutions diluées avec C < C_lim , de l'absorbance mesurée par le spectrophotomètre :

A = log (I₀ / I) = e l . l.C

2-2 Utilisation :

* Pour une espèce colorée, une concentration et une longueur d'onde données, A est affichée directement par le spectrophotomètre, après réglage du blanc (valeur I₀ avec, dans la cuve, la solution sans l'espèce colorée, remplacée par de l'eau distillée).

* En reliant le spectrophotomètre à une entrée COM (port série) d'un ordinateur muni du logiciel Synchrochim (extension utilisable, quand elle est installée, dans Synchronie par exécuter) on peut, après réglage du blanc :

pour une concentration donnée d'une espèce colorée, enregistrer le spectre d'absorbance, courbe A(l ) des variations de l'absorbance avec la longueur d'onde de la radiation utilisée et en déduire la valeur de l donnant l'absorbance maximale (pour cette espèce) ;

pour une valeur de l , enregistrer la courbe A(t) des variations de l'absorbance en fonction de la concentration au cours d'une réaction où cette espèce colorée est réactif ou produit ; et en tirer la courbe, C(t) = A(t) / (e l .l), permettant l'étude cinétique de cette réaction.

Remarque :

Les mesures d'un spectrophotomètre sont limitées par une absorbance maximale (souvent Amax = 2, soit I = I₀ / 100 avec 99 % de l'intensité lumineuse absorbée) : il faut donc choisir des conditions de réaction où la concentration maximale de l'espèce colorée n'entraîne pas la saturation du spectrophotomètre. Pour cela, on peut agir sur les concentrations des réactifs et aussi utiliser une longueur d'onde un peu éloignée de celle qui donne l'absorbance maximale pour cette espèce colorée.

2-3 Courbes de la réaction H₂O₂ + I^- :

2-3-1 Spectre d'absorbance de I₂, produit coloré de la réaction en présence excès de I^- :

Après réglage du blanc, le spectrophotomètre mesure l'absorbance pour des longueurs d'onde comprises entre 334 et 550 nm et trace la courbe A(l ) pour une solution I₂(avec excès I^-) de concentration C connue.

Le pic d'absorbance se trouve dans l'ultraviolet avec un maximum autour de 350 nm.

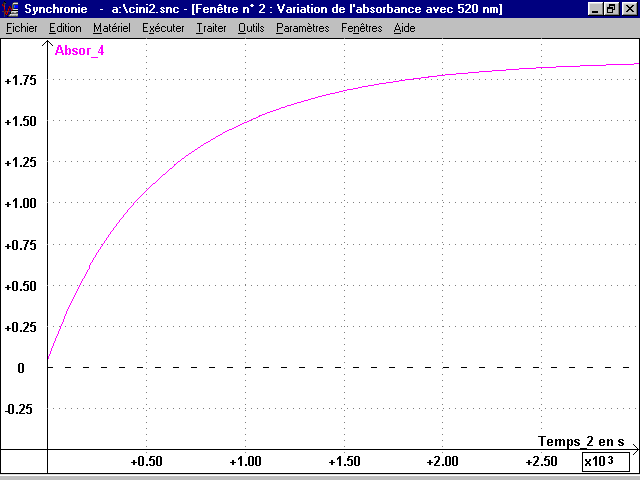
2-3-2 Courbes A(t), C(t), n(t) et v_fI₂(t) au cours de la réaction :

* Pour ne pas saturer le spectrophotomètre, on utilisera l = 520 nm. Pour cette valeur, on calcule, à partir de l'absorbance A mesurée pour une solution I₂ de concentration C et de bvolume V connus :

e l l = A / C = A / (n/V) et k = e l _..l.V = A / n = 0,191 (10^-5mol)^-1

La courbe A(t) est tracée à vue dans Synchronie. Comme C est proportionnelle à l'absorbance, la courbe A(t) donne l'allure des variations de C et de n = C.V au cours de la réaction ; et permet une étude qualitative de la cinétique de la réaction.

* Avec le coefficient de proportionnalité, A(t) permet aussi d'obtenir les courbes C(t) et n(t). Par exemple avec la feuille de calcul de Synchronie :

n(t) = n(I₂)(t) (10^-5mol) = A(t) / k = 5,23 A(t)

* La courbe v_fI₂(t) = v_d H₂O₂(t) est obtenue en dérivant n(t) par rapport au temps. Pour avoir une bonne courbe v_fI₂(t), il faut modéliser n(t) avant de la dériver (polynôme degré 6).

_________________________________________________________