Le P.I.B d'un pays connaît les variations suivantes : +3% ; -1% ; +5% ; +8% On souhaite calculer un taux de croissance annuel moyen de la production sur ces quatre années. Une moyenne arithmétique des taux serait mathématiquement inexacte (elle servira au mieux d'approximation).

Si t est le taux de croissance annuel moyen, cela signifie que tous les ans, la grandeur a augmenté de t % pendant n années. Ce qui revient à dire que chaque année, la grandeur a été multiplié par le coefficient multiplicateur noté :

(1 +

)

(Voir les règles de conversion pour passer du taux de variation au coefficient multiplicateur)

La progression globale de la grandeur est donc égale à :

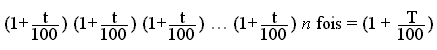
Cela signifie que chaque année, elle augmente de t % et (1 +T/100) est le coefficient multiplicateur global, c'est-à-dire permettant de passer de la valeur initiale à la valeur finale.

Exemple -  

Pour l'évolution du PIB citée au début de la fiche, On commence par calculer le coefficient multiplicateur global :

Cela signifie que le PIB a augmenté en moyenne de 3,7 % par an.

Remarque - 

Calcul des racines n^ième avec la calculatrice : Le calcul du taux de croissance annuel moyen dépend des touches de la calculatrice. Pour le calcul de l'exemple ci-dessus (les carrés correspondent aux touches de la calculatrice) :