Utilisation du menu CUSTOM menuz()

• Introduction et écran principal
• F1 Info
• F2 Calculs d'impédances
• F3 Passage structure série-structure parallèle
• F4 Passage structure parallèle-structure série
• F5 Remise à zéro
• F6 Calculs de modules et arguments
• F7 Diviseur de courant et de tension
• F8 Impédances équivalentes et résolutions
• Télécharger le programme pour TI92 et , pour TI89
  

Introduction et écran principal
Comme son nom l'indique presque, il sert à faciliter les calculs (numériques ou litteraux) utilisant les nombres complexes sur les impédances. Lancer le programme menuz() puis faire .
Refaire pour revenir au menu d'origine. Les nouveaux menus déroulants sont toujours présents au redémarrage s'ils n'ont pas été enlevés.

Les différentes fonctions:

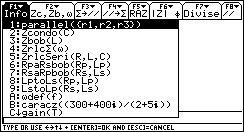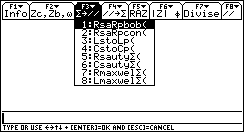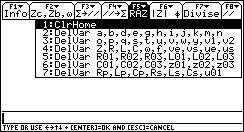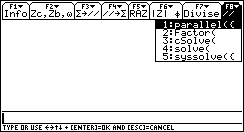
Appuyer sur le bouton stop(Netscape) ou Arrêter(IE4) de votre navigateur pour fixer un écran.

Retour debut page

F1 : Info
Observer le résultat de la fonction créée et savoir quelles sont les variables utilisées par cette fonction.
Retour debut page

F2 Calculs d'impédances:

• zcondo(C)renvoi l'impédance complexe de c:
• zbob(L) renvoi l'impédance complexe d'une inductance pure l: i.l.w
• ZrlcSeri(R,L,C) donne l'impédance complexe de R,L et C en série en fonction de w.
• ZrlcPara(R,L,C) idem pour RLC parallèle. Pour une forme compacte ajouter Factor( devant (F8-2).
• wdef(f) renvoi la pulsation w = 2.pi.f;

Retour debut page

F3 Passage de la structure série à la structure parallèle (//)

• RsaRpbob(rs,ls) passage de R_S à R_P pour une bobine définie par R_S et L_S .
• RsaRpcon(rs,cs) passage de R_S à R_P pour un condensateur défini par R_S et C_S.
• LstoLp(rs,lp) passage de L_S à L_P pour une bobine définie par R_S et L_S .
• RsautyS(p,q,r,c) détermine R_S du condensateur inconnu dans un pont de Sauty série (pont P/Q)
• RmaxwelS(p,q,r,c) détermine R_S de la bobine inconnue du pont de Maxwell (pont P.Q).

Retour debut page

F4 Passage de la structure parallèle (//) à la structure série
Rhayp(p,q,r,c) donne R_P de la bobine inconnue du pont de Hay (pont P.Q)
Pour le reste voir F3 à l'envers
Retour debut page

F5 Remise à zéro
Choisir le cas oportun. (pas terrible!) A partir du menu VAR-LINK sélectionner le répertoire dans lequel se trouve menuz(), sélectionner les variables : Var-type: Expr et les effacer.
Retour debut page

F6 |Z| f calculs de modules et arguments

• reelle(z) donne la partie réelle de z. (idem real(z), mais en français)
• caracz(z) affiche une boite avec le module et l'argument de Z, seulement en application numérique.
• gain(T) donne 20.log(T). Oui, oui 20.log(t) = 8,68588963806ln(t), j'ai vérifié!
• zrlcS(w) donne le module de RLC série.
• zrlcP(w) idem pour RLC parallèle.

Retour debut page

F7 Diviseur de tension et de courant:

• divtens(utotal,z1,z2): diviseur de tension: donne l'expression de la tension u₁ aux bornes de Z₁. u_total appliquée à Z₁ et Z₂ en série.
• divcour(itotal,z1,z2): diviseur de courant: donne l'expression du courant i₁ dans Z₁.
• divcourN(itotal,{z1,z2,z3...}): les courants dans Z₁, Z₂... et divcourN(itotal,{z1,z2,z3...})[2] pour le courant dans Z₂.
• superpos(v1,z1,z2,v2): théorème de superposition: donne la tension u entre Z₁ et Z₂ avec, à gauche (en entrée) v₁ et à droite (en sortie) v₂..

Retour debut page

F8 Impédances équivalentes et résolutions:
Calculs d'impédance équivalentes à des groupements parallèles: factor( est dans ce menu car la TI92 calcul toujours une impédance sous la forme a + i.b en fatorisant on peut espérer l'obtenir sous forme de quotient.

• parallel({z1,z2,z3}) calcul ou expression de l'impédance équivalente au groupement Z₁, Z₂ et Z₃ en parallèle.
• cSolve(: voir doc
• Solve(: voir exemple montage amplificateur inverseur à aop.
• syssolve({eq1,eq2...},{var1,var2...})
  Exemple:syssolve({x+2=3y,2y-4x=8},{x,y})
  Résultats: {x=2, y=0}.

Retour debut page

Retour page physique appliquée

Ecrivez-moi pour plus d'informations