Dans Regressi on obtient la représentation de y en fonction de x (figure 8).
Il ne faut pas tenir compte des éventuels messages d'erreur concernant les axes othonormés.
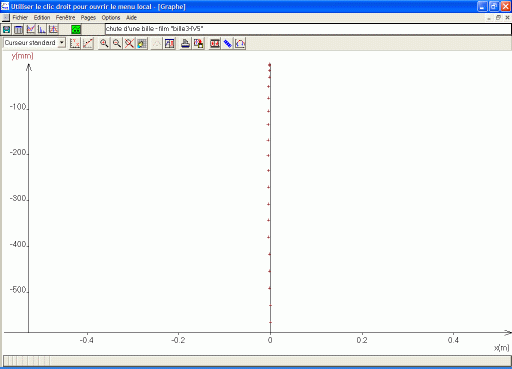
figure 8
|
Dans Regressi on obtient la représentation de y en fonction de x (figure 8). Il ne faut pas tenir compte des éventuels messages d'erreur concernant les axes othonormés.
|

figure 8 |
Avec l'orientation des axes choisie, la vitesse de chute est l'opposé de la dérivée de y par rapport au temps.
Il faut opérer en deux étapes : calculer la dérivée puis changer le signe.
Passer dans la fenêtre des grandeurs de Regressi en cliquant
sur ![]() .
.
Choisir "Ajouter une grandeur" en cliquant sur ![]() .
.
|
Dans un premier temps on va calculer la dérivée de y par rapport au temps. La nouvelle grandeur doit être de type "Dérivée". La nommer, par exemple, "dery" et la définir comme dy/dt (figure 9). Cliquer sur OK. |
 figure 9 |
On va maintenant calculer la vitesse. Pour cela il faut ajouter
une autre grandeur en cliquant de nouveau sur ![]() .
.
|
Choisir cette fois une "Grandeur calculée", la nommer v et la définir comme l'opposé de la dérivée précédente (figure 10). Cliquer sur OK. |
 figure 10 |
|
Passer dans l'onglet "Variables" Il y a les valeurs des dates, de x, de y, de la dérivées de y par rapport au temps et celles de la vitesse (figure 11). |
|
|
Repasser dans la fenêtre "Graphique" en
cliquant sur Afficher la fenêtre des coordonnées en cliquant
sur Choisir maintenant de représenter la vitesse v en fonction du temps t avec une ligne de type "Lissage" d'ordre "3" et des points tracés par des "Croix" (figure 12) . Cliquer sur OK.
|
 figure 12 |
|
On obtient la courbe souhaitée (figure 13). Sur cette courbe on distingue bien le régime transitoire (vitesse croissante) et le régime permanent (vitesse constante). |
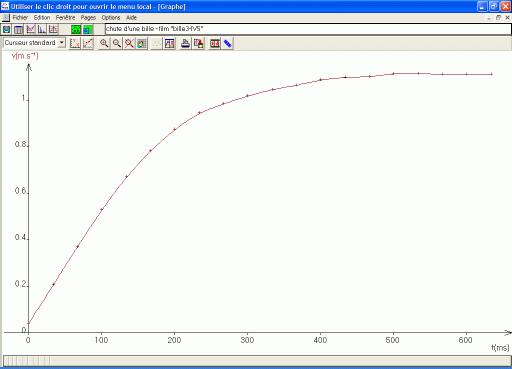 figure 13 |
La vitesse initiale est rarement nulle car le début du mouvement n'est pas synchronisé avec la prise d'une image.